1 、甲、乙、丙三个单位各派2名志愿者参加公益活动,现将这6人随机分成3组,每组2人,则每组成员均来自不同单位的概率是:
A.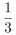
B.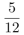
C.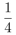
D.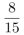
解析
解法一:
第一步,本题考查概率问题,属于基本概率。
第二步,首先在6人中随机选取1人,概率为1,剩下的5人中只有4人可与其一组,则第一组两人来自不同单位的概率为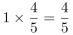 ;再在4人中随机选取1人,概率为1,剩下的3人只有2人可与其一组,则第二组两人来自不同单位的概率为
;再在4人中随机选取1人,概率为1,剩下的3人只有2人可与其一组,则第二组两人来自不同单位的概率为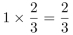 ;最后一组的两人也一定来自不同单位,故每组成员均来自不同单位的概率为
;最后一组的两人也一定来自不同单位,故每组成员均来自不同单位的概率为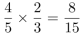 。
。
因此,选择D选项。
解法二:
第一步,本题考查概率问题,属于基本概率。
第二步,将6个人随机分成3组,总的情况数为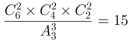 (种)。每组成员来自不同单位,只能是(甲,乙)、(甲,丙)、(乙,丙)配对,共有
(种)。每组成员来自不同单位,只能是(甲,乙)、(甲,丙)、(乙,丙)配对,共有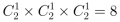 (种)情况。
(种)情况。
第三步,每组成员均来自不同单位的概率为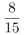 。
。
因此,选择D选项。
2、一艘游轮在海上匀速航行,航向保持不变。上午8时在游轮的正东方30海里处有一灯塔,上午10时30分该灯塔位于游轮的正南方40海里处,则在该时段内,游轮与灯塔距离最短的时刻是:
A.8时45分
B.8时54分
C.9时15分
D.9时18分
解析
第一步,本题考查几何问题,属于几何特殊性质类。
第二步,如图,游轮从A点运动到C点,在直角△ABC中,AB=30,BC=40,由勾股定理AB²+BC²=AC²可知,AC=50。过B作AC垂线交于D点,BD即为游轮与灯塔的最短距离。根据三角形相似判定定理可知△ADB∽△ABC,可得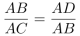 ,解得AD=18。
,解得AD=18。

第三步,游轮航行50海里用时2.5小时,则航行18海里用时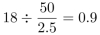 (小时),即0.9×60=54(分钟),故游轮与灯塔距离最短的时刻是8时54分。
(小时),即0.9×60=54(分钟),故游轮与灯塔距离最短的时刻是8时54分。
因此,选择B选项。
3、小王去超市购物,带现金245元,其中1元6张、2元2张、5元3张、10元2张、50元2张、100元1张,选购的物品总计167元。若用现金结账且不需要找零,则不同的面值组合方式有:
A.6种
B.7种
C.8种
D.9种
解析
第一步,本题考查排列组合问题,属于基础排列组合,用枚举法解题。
第二步,除了50元和100元,其他钱的总和为45元,故167元中必然包含一张100元与一张50元,只需讨论余下17元的组合方式即可。枚举如下表:
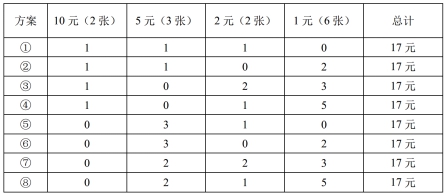
故一共有8种组合方式。
因此,选择C选项。
4 、玩具厂原来每日生产玩具560件,用A、B两种型号的纸箱装箱,正好装满24只A型纸箱和25只B型纸箱。扩大生产规模后该玩具的日产量翻了一番,仍然用A、B两种型号的纸箱装箱,则每日需要纸箱的总数至少是:
A.70只
B.75只
C.77只
D.98只
解析
第一步,本题考查不定方程问题。
第二步,设A、B型纸箱各能装下a件、b件玩具,根据题意可得:24a+25b=560。由于24a与560均能被8整除,则b也能被8整除。当b=8时,解得a=15,满足等式要求;当b=16,a为非整数,排除;当b=24,a<0,排除。则确定每个A型纸箱能装下15件玩具,每个B型纸箱能装下8件玩具。
第三步,要想日产量翻番后,纸箱总数尽量少,则容量大的A型箱应尽可能多用。设A、B型纸箱各用了x、y只,根据题意可列方程:15x+8y=560×2,移项可得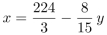 ,当y=0时,x≈74.7取得最大值,则每日需要纸箱的总数至少是75只。
,当y=0时,x≈74.7取得最大值,则每日需要纸箱的总数至少是75只。
因此,选择B选项。
5、如图,在梯形ABCD中,AB=2,CD=3,AC交BD于O点,过O作AB的平行线交BC于E点,连接DE交AC于F点,过F作AB的平行线交BC于G点,连接DG交AC于M点,过M作AB的平行线交BC于N点,则线段MN的长为( )。

A.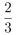
B.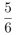
C.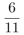
D.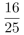
解析
第一步,本题考查几何问题,属于几何特殊性质类。
第二步,在梯形ABCD中,由三角形相似判定定理可知,△AOB∽△COD,则有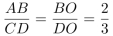 ;同时△BEO∽△BCD,则有
;同时△BEO∽△BCD,则有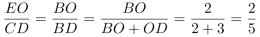 。
。
第三步,同理可得,在梯形OECD中,△OFE∽△CFD,则有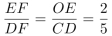 ;同时△EGF∽△ECD,则
;同时△EGF∽△ECD,则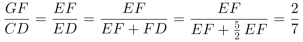 。
。
第四步,同理可得,在梯形FGCD中,△FGM∽△CDM,则有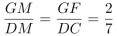 ;同时△GNM∽△GCD,则
;同时△GNM∽△GCD,则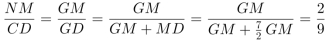 ,已知DC=3,则
,已知DC=3,则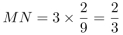 。
。
因此,选择A选项。
6 、某公司将一款自行车3次折价销售,第二次在首次打折的基础上打相同的折扣,第三次在第二次打折的基础上降价三分之一。已知该款自行车3次折扣后的价格是原价的54%,则首次的折扣是:
A.7.5折
B.8折
C.8.4折
D.9折
解析
第一步,本题考查经济利润问题,属于利润率折扣类。
第二步,赋值原价为100,设首次折扣为a,根据三次打折后价格是原价的54%,得 ,解得a=0.9,即9折。
,解得a=0.9,即9折。
因此,选择D选项。
7 、若将一项工程的1/6、1/4、1/3、1/4,依次分配给甲、乙、丙、丁四家工程队,分别需要15天、15天、30天和9天完成,则他们合作完成该项工程需要的时间是:
A.12天
B.15天
C.18天
D.20天
解析
第一步,本题考查工程问题,属于时间类。
第二步,甲需要15天完成工程的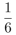 ,则甲完成整个工程要
,则甲完成整个工程要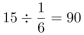 (天),同理乙、丙、丁完成整个工程分别需要60、90、36天,故赋值工作总量为180(90、60、90、36的公倍数),那么甲队工作效率为180÷90=2,同理乙、丙、丁的工作效率分别为3、2、5。
(天),同理乙、丙、丁完成整个工程分别需要60、90、36天,故赋值工作总量为180(90、60、90、36的公倍数),那么甲队工作效率为180÷90=2,同理乙、丙、丁的工作效率分别为3、2、5。
第三步,甲、乙、丙、丁四队合作完成该项工程需要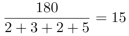 (天)。
(天)。
因此,选择B选项。
8、一个圆盘上按顺时针方向依次排列着编号为1到7的七盏彩灯,通电后每个时刻只有三盏亮着,每盏亮6秒后熄灭,同时其顺时针方向的下一盏灯开始亮,如此反复。若通电时编号为1,3,5的三盏先亮,则200秒后亮着的三盏彩灯的编号是:
A.1,3,6
B.1,4,6
C.2,4,7
D.2,5,7
解析
解法一:
第一步,本题考查循环周期问题。
第二步,由题可知,初始时(1,3,5)先亮,6秒后(2,4,6)亮,再6秒后(3,5,7)亮…则200秒内转换200÷6=33…2,即33次。
第三步,圆盘上共7盏灯,即转换7次为一个循环周期,33÷7=4…5,相当于从初始状态按顺时针往下转换5次,此时1号灯变为6(1→2→3→4→5→6),3号灯变为1(3→4→5→6→7→1),5号灯变为3(5→6→7→1→2→3),即200秒后亮着的三盏彩灯的编号是(1,3,6)。
因此,选择A选项。
解法二:
第一步,本题考查循环周期问题。
第二步,由题可知,每6秒亮灯顺序依次为(1,3,5)(2,4,6)(3,5,7)(4,6,1)(5,7,2)(6,1,3)(7,2,4)(1,3,5)…,可发现共转7次回到初始状态,则一个周期需要的时间为6×7=42(秒)。200÷42=4…32,故200秒即为4个周期后的32秒,32÷6=5…2,相当于从初始状态按顺时针往下转换5次,为(6,1,3)亮灯。
因此,选择A选项。
9、某公司管理人员、技术人员和后勤服务人员一月份的平均收入分别为6450元、8430元和4350元,收入总额分别为5.16万元、33.72万元和5.22万元,则该公司这三类人员一月份的人均收入是:
A.6410元
B.7000元
C.7350元
D.7500元
解析
第一步,本题考查平均数问题。
第二步,根据题意可得,管理人员有51600÷6450=8(人),技术人员有337200÷8430=40(人),后勤服务人员有52200÷4350=12(人)。
第三步,该公司这三类人员一月份的人均收入为 (元)。
(元)。
因此,选择C选项。
10、某一楼一户住宅楼共17层,电梯费按季度缴纳,分摊规则为:第一层的住户不缴纳;第二层及以上的住户,每层比下一层多缴纳10元。若第一季度该住宅楼某单元的电梯费共计1904元,则该单元第7层住户一季度应缴纳的电梯费是:
A.72元
B.82元
C.84元
D.94元
解法一:
第一步,本题考查数列问题。
第二步,根据每层比下一层多缴纳10元可知,第2—17层的缴费金额为公差是10的等差数列,设第一季度第2层缴费金额为x,则第17层所缴金额为x+(17-2)×10=x+150。根据电梯费共计1904元,可得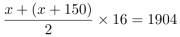 ,解得x=44。
,解得x=44。
第三步,第7层缴费金额为44+(7-2)×10=94(元)。
因此,选择D选项。
解法二:
第一步,本题考查数列问题。
第二步,2—17层的所缴金额构成一个16项的等差数列,中间项是第 (项),中位数为
(项),中位数为 ,即第9.5层需缴119元。由于公差是10,故第7层的缴费金额是119-(9.5-7)×10=94(元)。
,即第9.5层需缴119元。由于公差是10,故第7层的缴费金额是119-(9.5-7)×10=94(元)。
因此,选择D选项。
A.
B.
C.
D.
解析
解法一:
第一步,本题考查概率问题,属于基本概率。
第二步,首先在6人中随机选取1人,概率为1,剩下的5人中只有4人可与其一组,则第一组两人来自不同单位的概率为
因此,选择D选项。
解法二:
第一步,本题考查概率问题,属于基本概率。
第二步,将6个人随机分成3组,总的情况数为
第三步,每组成员均来自不同单位的概率为
因此,选择D选项。
2、一艘游轮在海上匀速航行,航向保持不变。上午8时在游轮的正东方30海里处有一灯塔,上午10时30分该灯塔位于游轮的正南方40海里处,则在该时段内,游轮与灯塔距离最短的时刻是:
A.8时45分
B.8时54分
C.9时15分
D.9时18分
解析
第一步,本题考查几何问题,属于几何特殊性质类。
第二步,如图,游轮从A点运动到C点,在直角△ABC中,AB=30,BC=40,由勾股定理AB²+BC²=AC²可知,AC=50。过B作AC垂线交于D点,BD即为游轮与灯塔的最短距离。根据三角形相似判定定理可知△ADB∽△ABC,可得

第三步,游轮航行50海里用时2.5小时,则航行18海里用时
因此,选择B选项。
3、小王去超市购物,带现金245元,其中1元6张、2元2张、5元3张、10元2张、50元2张、100元1张,选购的物品总计167元。若用现金结账且不需要找零,则不同的面值组合方式有:
A.6种
B.7种
C.8种
D.9种
解析
第一步,本题考查排列组合问题,属于基础排列组合,用枚举法解题。
第二步,除了50元和100元,其他钱的总和为45元,故167元中必然包含一张100元与一张50元,只需讨论余下17元的组合方式即可。枚举如下表:

故一共有8种组合方式。
因此,选择C选项。
4 、玩具厂原来每日生产玩具560件,用A、B两种型号的纸箱装箱,正好装满24只A型纸箱和25只B型纸箱。扩大生产规模后该玩具的日产量翻了一番,仍然用A、B两种型号的纸箱装箱,则每日需要纸箱的总数至少是:
A.70只
B.75只
C.77只
D.98只
解析
第一步,本题考查不定方程问题。
第二步,设A、B型纸箱各能装下a件、b件玩具,根据题意可得:24a+25b=560。由于24a与560均能被8整除,则b也能被8整除。当b=8时,解得a=15,满足等式要求;当b=16,a为非整数,排除;当b=24,a<0,排除。则确定每个A型纸箱能装下15件玩具,每个B型纸箱能装下8件玩具。
第三步,要想日产量翻番后,纸箱总数尽量少,则容量大的A型箱应尽可能多用。设A、B型纸箱各用了x、y只,根据题意可列方程:15x+8y=560×2,移项可得
因此,选择B选项。
5、如图,在梯形ABCD中,AB=2,CD=3,AC交BD于O点,过O作AB的平行线交BC于E点,连接DE交AC于F点,过F作AB的平行线交BC于G点,连接DG交AC于M点,过M作AB的平行线交BC于N点,则线段MN的长为( )。

A.
B.
C.
D.
解析
第一步,本题考查几何问题,属于几何特殊性质类。
第二步,在梯形ABCD中,由三角形相似判定定理可知,△AOB∽△COD,则有
第三步,同理可得,在梯形OECD中,△OFE∽△CFD,则有
第四步,同理可得,在梯形FGCD中,△FGM∽△CDM,则有
因此,选择A选项。
6 、某公司将一款自行车3次折价销售,第二次在首次打折的基础上打相同的折扣,第三次在第二次打折的基础上降价三分之一。已知该款自行车3次折扣后的价格是原价的54%,则首次的折扣是:
A.7.5折
B.8折
C.8.4折
D.9折
解析
第一步,本题考查经济利润问题,属于利润率折扣类。
第二步,赋值原价为100,设首次折扣为a,根据三次打折后价格是原价的54%,得
因此,选择D选项。
7 、若将一项工程的1/6、1/4、1/3、1/4,依次分配给甲、乙、丙、丁四家工程队,分别需要15天、15天、30天和9天完成,则他们合作完成该项工程需要的时间是:
A.12天
B.15天
C.18天
D.20天
解析
第一步,本题考查工程问题,属于时间类。
第二步,甲需要15天完成工程的
第三步,甲、乙、丙、丁四队合作完成该项工程需要
因此,选择B选项。
8、一个圆盘上按顺时针方向依次排列着编号为1到7的七盏彩灯,通电后每个时刻只有三盏亮着,每盏亮6秒后熄灭,同时其顺时针方向的下一盏灯开始亮,如此反复。若通电时编号为1,3,5的三盏先亮,则200秒后亮着的三盏彩灯的编号是:
A.1,3,6
B.1,4,6
C.2,4,7
D.2,5,7
解析
解法一:
第一步,本题考查循环周期问题。
第二步,由题可知,初始时(1,3,5)先亮,6秒后(2,4,6)亮,再6秒后(3,5,7)亮…则200秒内转换200÷6=33…2,即33次。
第三步,圆盘上共7盏灯,即转换7次为一个循环周期,33÷7=4…5,相当于从初始状态按顺时针往下转换5次,此时1号灯变为6(1→2→3→4→5→6),3号灯变为1(3→4→5→6→7→1),5号灯变为3(5→6→7→1→2→3),即200秒后亮着的三盏彩灯的编号是(1,3,6)。
因此,选择A选项。
解法二:
第一步,本题考查循环周期问题。
第二步,由题可知,每6秒亮灯顺序依次为(1,3,5)(2,4,6)(3,5,7)(4,6,1)(5,7,2)(6,1,3)(7,2,4)(1,3,5)…,可发现共转7次回到初始状态,则一个周期需要的时间为6×7=42(秒)。200÷42=4…32,故200秒即为4个周期后的32秒,32÷6=5…2,相当于从初始状态按顺时针往下转换5次,为(6,1,3)亮灯。
因此,选择A选项。
9、某公司管理人员、技术人员和后勤服务人员一月份的平均收入分别为6450元、8430元和4350元,收入总额分别为5.16万元、33.72万元和5.22万元,则该公司这三类人员一月份的人均收入是:
A.6410元
B.7000元
C.7350元
D.7500元
解析
第一步,本题考查平均数问题。
第二步,根据题意可得,管理人员有51600÷6450=8(人),技术人员有337200÷8430=40(人),后勤服务人员有52200÷4350=12(人)。
第三步,该公司这三类人员一月份的人均收入为
因此,选择C选项。
10、某一楼一户住宅楼共17层,电梯费按季度缴纳,分摊规则为:第一层的住户不缴纳;第二层及以上的住户,每层比下一层多缴纳10元。若第一季度该住宅楼某单元的电梯费共计1904元,则该单元第7层住户一季度应缴纳的电梯费是:
A.72元
B.82元
C.84元
D.94元
解法一:
第一步,本题考查数列问题。
第二步,根据每层比下一层多缴纳10元可知,第2—17层的缴费金额为公差是10的等差数列,设第一季度第2层缴费金额为x,则第17层所缴金额为x+(17-2)×10=x+150。根据电梯费共计1904元,可得
第三步,第7层缴费金额为44+(7-2)×10=94(元)。
因此,选择D选项。
解法二:
第一步,本题考查数列问题。
第二步,2—17层的所缴金额构成一个16项的等差数列,中间项是第
因此,选择D选项。










